1) 직접 주소화 방법의 단점과 해시 테이블
- 직접 주소화 방법의 단점은 명백하다. 전체 집합 U가 크다면 일반적인 컴퓨터의 메모리 공간에서는
크기 |U|가 가지는 테이블 T를 저장하는 것은 비실용적이거나 불가능하다.
게다가 실제 저장되는 키들의 집합 K는 U에 비해 상대적으로 작아서
T를 위해 할당된 대부분의 공간은 낭비된다.
- 사전에 저장된 키들의 집합 K가 모든 가능한 키들의 전체 집합 U에 비해 훨씬 작을 때,
해시 테이블은 직접 주소 테이블보다 훨씬 작은 공간을 필요로 한다.
- 특히, 원소의 검색에 소요되는 시간이 단지 O(1)인 이점을 유지하면서 사용 저장 공간을 O(|K|)로 줄일 수 있다.
다만, 직접 주소화 방법에서는 이 수행시간이 최악의 경우 수행시간에 해당되지만
해시 테이블을 이용한 방법에서는 이것이 평균 수행시간이 된다.
- 직접 주소화 방법에서 키 k를 갖는 원소가 위치 k에 저장된다.
그리고 해싱을 이용한 방법에서는 키 k를 갖는 원소는 위치 h(k)에 저장된다.
즉, 키로부터 저장될 위치를 계산하기 위해 해시 함수 h를 사용한다.
여기서 h는 키들의 전체 집합 U를 해시 테이블 T[0...m-1]의 각 위치에 대응시킨다.
h : U -> {0, 1, ... m-1|
- 이 때, 해시 테이블의 크기 m은 일반적으로 |U|보다 훨씬 작다.
"키 k를 갖는 원소가 위치 h(k)에 해시된다"고 말하고, "h(k)는 키 k의 해시 값이다"라고 한다.
- 아래 그림은 기본 아이디어를 설명한다.
해시 함수는 배열의 인덱스 범위를 줄이게 되어 배열의 크기를 줄이게 된다.
배열은 |U|의 크기 대신 크기 m을 가진다.
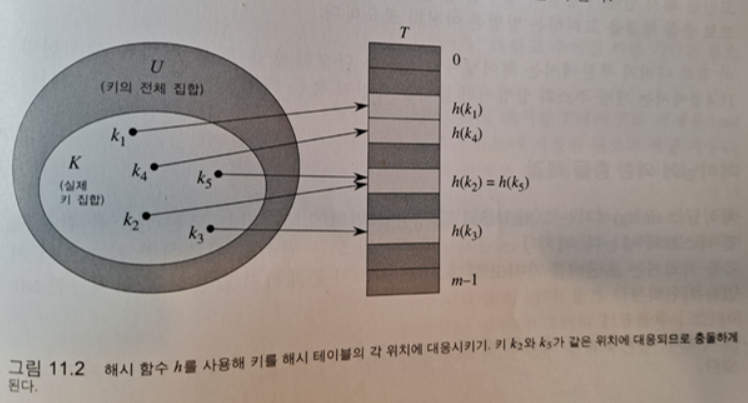
2) 해시 충돌
-해싱을 이용하는 경우 키 두 개가 동일한 위치에 해시될 수 있는 단점이 있다.
이 상황을 해시 충돌이라 한다. 다행히 충돌에 의해 발생하는 문제를 해결하는 효율적인 방법이 있다.
- 물론, 이상적인 해결법은 충돌을 완전히 피하는 것이다.
이를 위해서는 적절한 해시함수 h를 선택하는 것이 중요하다.
한 가지 방안은 "무작위"인것처럼 보이는 함수 h를 사용해 충돌을 피하거나 충돌의 횟수를 줄이는 것이다.
'Introduction to Algorithms' 카테고리의 다른 글
| [Introduction to Algorithms] 이진 검색 트리 (0) | 2024.09.18 |
|---|---|
| [Introduction to Algorithms] 해시 테이블 - 체이닝에 의한 충돌 해결 (0) | 2024.06.29 |
| [Introduction to Algorithms] 동적 프로그래밍 (0) | 2024.06.29 |
| [Introduction to Algorithms] 랜덤화된 퀵 정렬 (0) | 2024.06.29 |
| [Introduction to Algorithms] 퀵 정렬 - 퀵 정렬의 성능 (0) | 2024.06.23 |
