1) 서문
- 이번 장에서는 신경망 학습의 핵심 개념들을 만나봅니다. 이번 장에서 다룰 주제는 가중치 매개변수의 최적값을 탐색하는
최적화 방법, 가중치 매갭녀수 초깃값, 하이퍼파라미터 설정 방법 등 모두가 신경망 학습에서 중요한 주제입니다.
오버피팅의 대응책인 가중치 감소와 드롭아웃등의 정규화 방법도 간략히 설명하고 구현해봅니다.
마지막으로 최근 많은 연구에서 사용하는 배치 정규화도 짧게 알아봅니다.
이번 장에서 설명하는 기법을 이용하면 신경망(딥러닝) 학습의 효율과 정확도를 높일 수 있습니다.
그럼 본론으로 들어가 볼까요?
2) 매개변수 갱신
- 신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것이었죠.
이는 곧 매개변수의 최적값을 찾는 문제이며, 이러한 문제를 푸는 것을 최적화(optimization)이라 합니다.
안타깝게도 신경망 최적화는 굉장히 어려운 문제입니다.
매개변수 공간은 매우 넓고 복잡해서 최적의 솔루션은 쉽게 못 찾으니까요.
수식을 풀어 순식간에 최솟값을 구하는 방법 같은 것은 없습니다.
게다가 심층 신경망에서는 매개변수의 수가 엄청나게 많아져서 사태는 더욱 심각해집니다.
- 우리는 지금까지 최적의 매개변수 값을 찾는 단서로 매개변수의 기울기(미분)를 이용했습니다.
매개변수의 기울기를 구해, 기울어진 방향으로 매개변수 값을 갱신하는 일을 몇 번이고 반복해서
점점 최적의 값에 다가갔습니다.
이것이 확률적 경사 하강법(SGD)이란 단순한 방법인데, 매개변수 공간을 무작정 찾는 것보다 '똑똑한' 방법입니다.
SGD는 단순하지만, (문제에 따라서는) SGD보다 똑똑한 방법도 있답니다.
지금부터 SGD의 단점을 알아본 후 SGD와는 다른 최적화 기법을 소개하려 합니다.
2-1) 모험가 이야기
- 본론으로 들어가기 전에 최적화를 해야 하는 우리의 상황을 모험가 이야기에 비유해보겠습니다.
색다른 모험가가 있습니다. 광활한 메마른 산맥을 여행하면서 날마다 깊은 골짜기를 찾아 발걸음을 옮깁니다.
그는 전설에 나오는 세상에서 가장 깊고 낮은 골짜기, '깊은 곳'을 찾아가려 합니다. 그것이 그의 여행 목적이죠.
게다가 그는 엄격한 '제약' 2개로 자신을 옭아맸습니다.
하나는 지도를 보지 않을 것, 또 하나는 눈가리개를 쓰는 것입니다.
지도도 없고 보이지도 않으니 가장 낮은 골짜기가 광대한 땅 어디에 있는지 알 도리가 없죠.
그런 혹독한 조건에서 이 모험가는 어떻게 '깊은 곳'을 찾을 수 있을까요?
어덯게 걸음을 옮겨야 효율적으로 '깊은 곳'을 찾아낼 수 있을까요?
- 최적 매개변수를 탐색하는 우리도 이 모험가와 같은 어둠의 세계를 탐험하게 됩니다.
광대하고 복잡한 지형을 지도도 없이 눈을 가린 채로 '깊은 곳'을 찾지 않으면 안됩니다.
척 봐도 어려운 문제임이 느껴지지 않나요?
- 이 어려운 상황에서 중요한 단서가 되는 것이 땅의 '기울기'입니다.
모험가는 주위 경치는 볼 수 없지만 지금 서 있는 당의 기울기는 알 수 있습니다.
발바닥으로 전해지죠. 그래서 지금 서 있는 장소에서 가장 크게 기울어진 방향으로 가자는 것이 SGD의 전략입니다.
이 일을 반복하면 언젠가 '깊은 곳'에 찾아갈 수 있을지도 모르죠.
적어도 용감한 모험가는 그렇게 생각할지도 모릅니다.
2-2) 확률적 경사 하강법(SGD)
- 최적화 문제의 어려움을 되새기고자 먼저 SGD를 복습해보겠습니다. SGD는 수식으로는 다음과 같이 쓸 수 있습니다.
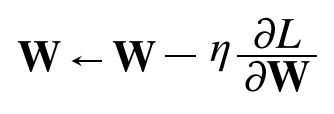
- 여기에서 W는 갱신할 가중치 매개변수고, oL/oW는 W에 대한 손실 함수의 기울기입니다. n는 학습률을 의미하는데,
실제로는 0.01이나 0.001과 같은 값을 미리 정해서 사용합니다. 또 <-는 우변의 값으로 좌변의 값을 갱신하다는 뜻입니다.
[식 6.1]에서 보듯 SGD는 기울어진 방향으로 일정 거리만 가겠다는 단순한 방법입니다.
그러면 이 SGD를 파이썬 클래스로 구현해보죠.
(나중에 사용할 것을 생각해 클래스 이름도 SGD로 했습니다)
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.key():
params[key] -= self.lr * grads[key]
- 초기화 때 받는 인수인 lr은 learning rate(학습률)를 뜻합니다. 이 학습률을 인스턴스 변수로 유지합니다.
update(params, grads) 메서드는 SGD 과정에서 반복해서 불립니다.
인수인 params와 grads는 (지금까지의 신경망 구현과 마찬가지로) 딕셔너리 변수입니다.
params['W1'], grads['W1']등과 같이 각각 가중치 매개변수와 기울기를 저장하고 있습니다.
- SGD 클래스를 사용하면 신경망 매개변수의 진행을 다음과 같이 수행할 수 있습니다.
(다음 코드는 실제로는 동작하지 않는 의사 코드입니다)
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
x_batch, y_batch = get_mini_batch(...) #미니배치
grads = network.gradient(x_batch, y_batch)
params = network.params
optimizer.update(params, grads)
- optimizer는 '최적화를 행하는 자'라는 뜻의 단어입니다. 이 코드에서는 SGD가 그 역할을 합니다. 매개변수 갱신은 optimizer가
책임지고 수행하니 우리는 optimizer에 매개변수와 기울기 정보만 넘겨주면 되는 것이죠.
이처럼 최적화를 담당하는 클래스를 분리해 구현하면 기능을 모듈화하기 좋습니다.
예를 들어, 곧이어 소개할 모멘텀이라는 최적화 기법 역시 update(params, grads)라는 공통의 메서드를 갖도록 구현합니다.
그 때, optimizer = SGD() 문장을 optimizer = Momentum()으로만 변경하면 SGD가 모멘텀으로 바뀌는 것이죠
3) SGD의 단점
- SGD는 단순하고 구현도 쉽지만, 문제에 따라서는 비효율적일 때가 있습니다.
이번 절에서는 SGD의 단점을 알아보고자 다음 함수의 최솟값을 구하는 문제를 생각해보겠습니다.
f(x, y) = 1/20x^2 + y^2 [식 6.2]
- 이 함수는 [그림 6-1]의 왼쪽과 같이 '밥그릇'을 x축 방향으로 늘인 듯한 모습이고, 실제로 그 등고선은 오른쪽과 같이
x축 방향으로 늘인 타원으로 되어 있습니다.
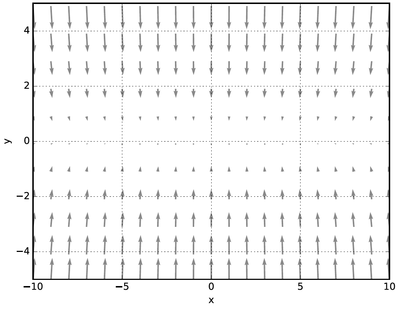
- [식 6.2] 함수의 기울기를 그려보면 [그림 6-2]처럼 됩니다. 이 기울기는 y축 방향은 크고 x축 방향은 작다는 것이 특징입니다.
말하자면 y축 방향은 가파른데 x축 방향은 완만한 것이죠.
또, 여기에서 주의할 점으로는 [식 6.2]가 최솟값이 되는 장소는 (x,y) = (0, 0) 이지만,
[그림 6-2]가 보여주는 기울기 대부분은 (0, 0) 방향을 가리키지 않는다는 것입니다.
- 이제 [그림 6-1]의 함수에 SGD를 적용해볼까요? 탐색을 시작하는 장소(초깃값)는 (x,y) = (-7.0, 2.0)으로 하겠습니다.
결과는 [그림 6-3]처럼 됩니다.
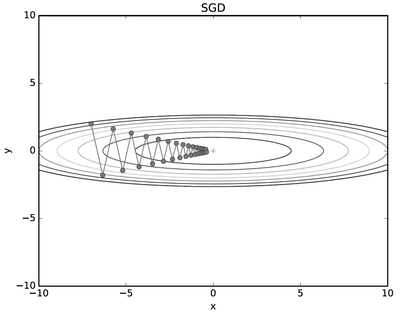
- SGD는 [그림 6-3]과 같은 심하게 굽이진 움직임을 보여주죠. 상당히 비효율적인 움직임입니다.
즉, SGD의 단점은 비등방성 함수(방향에 따라 성질, 즉 여기에서는 기울기가 달라지는 함수)에서는
탐색 경로가 비효율적이라는 것입니다. 이럴 때는 SGD 같이 무작정 기울어진 방향으로 진행하는 단순한
방식보다 더 영리한 묘안이 간절해집니다.
또한, SGD가 지그재그로 탐색하는 근본 원인은 기울어진 방향이 본래의 최솟값과 다른 방향을 가리켜서라는 점도
생각해볼 필요가 있습니다.
- 이제부터 SGD의 이러한 단점을 개선해주는 모멘텀, AdaGrad, Adam이라는 세 방법을 소개할 겁니다.
이들은 모두 SGD를 대체하는 기법으로, 각각을 간단히 설명하면서 수식과 파이썬 구현을 살펴보겠습니다.
'밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] 오차역전파법 (0) | 2024.08.25 |
|---|
