- 재귀는 3가지 관점에서 접근할 수 있습니다.
그것은 점화식 관점, 분할 관점, 백트래킹 관점입니다.
각각에 대해 좀 더 자세히 살펴보겠습니다.
1) 점화식 관점
- 재귀를 잘 이해하려면 첫번째로 점화식으로 이해할 수 있습니다.
예를 들어, 다음과 같은 시그마를 계산하면 15라는 결과값을 얻을 수 있습니다.

- 그렇다면 시그마를 어떻게 재귀로 표현할 수 있을지 고민해보겠습니다.
점화식의 각 단계를 표현하면 다음과 같습니다.

- 그리고 점화식을 재귀적 구문의 코드로 작성하면 다음과 같습니다.
이 때, if(5 < n)은 재귀적 구문의 중단 조건입니다.

- 그리고 n=1부터 시작한다면, 다음과 같이 순서대로 함수가 호출됩니다.

2) 분할 관점
- 분할 관점은 재귀적인 점화식을 포함할 수도 있지만, 점화식으로 딱 떨어져 나오는 것이 아닌
큰 문제를 작은 문제로 분할한 후, 작은 문제를 해결해서 큰 문제를 해결하는 방식입니다.
알고리즘 파트에서는 이것을 분할정복이라고 합니다 .
분할 관점을 잘 이해하면 병합 정렬(merge sort)도 쉽게 이해할 수 있습니다.
예를 들어, 배열의 총합을 구하기 위해, 분할 방식으로 배열을 최대한 쪼갠 후,
쪼개진 값들을 다 더해서 배열의 총합을 구할 수 있습니다.

- 우선은 배열의 길이에 따라, 길이가 짝수인 경우와 홀수인 경우로 나누어 볼 수 있습니다.
각각의 경우에 다음과 같이 분할 기준을 잡을 수 있습니다.
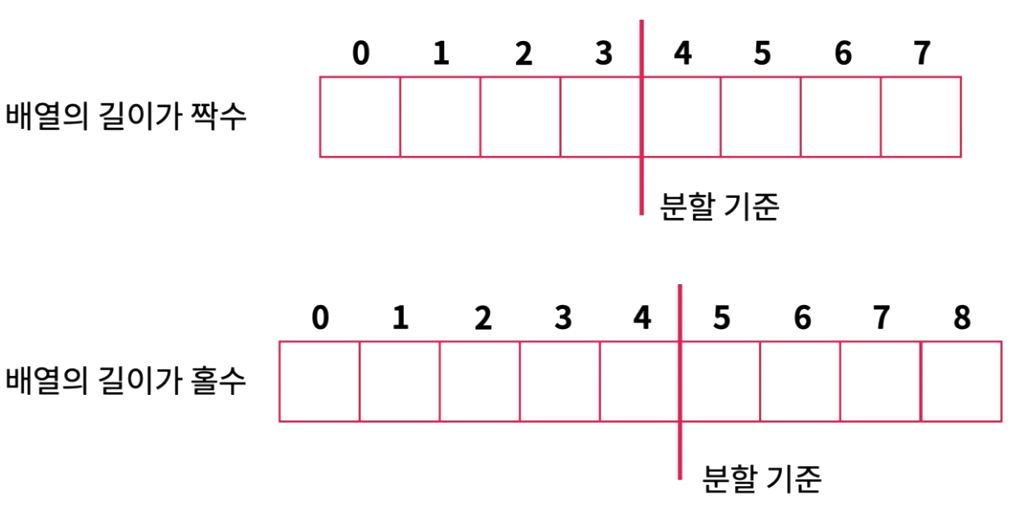
- 그리고 분할 관점에서는 다음과 같이 재귀적으로 분할 기준(=중앙값)을 구할 수 있습니다.
첫번째는 3, 두번째는 5, 세번째는 6이 각각 분할 기준이 됩니다.

- 이를 split이라는 함수와 도식도로 나타내면 다음과 같습니다.
split 메소드가 쪼개지면 최종적으로 쪼갤 수 없는 값이 1개인 배열이 됩니다.


- 그리고 split된 배열의 값들을 더한다면 다음과 같이 더해집니다.


3) 백트레킹 관점
- 백트레킹은 탐색 관점에서 스택의 특징을 이용하여 이전 분기로 돌아가 탐색하는 것을 의미합니다.
쉽게 말하면 게임을 하다가 특정 시점에서 세이브를 하고, 불러오기를 통해 다시 세이브 포인트로 돌아가 진행하는
것과 유사합니다.
참고
- 코드라떼 자료구조
'알고리즘' 카테고리의 다른 글
| 이진 트리 순회[너비 우선 탐색] (0) | 2022.09.08 |
|---|---|
| 이진트리 순회(깊이 우선 탐색) (0) | 2022.09.08 |
| 완전 탐색 기초 (0) | 2022.08.21 |
| 재귀 함수 (0) | 2022.08.01 |
| 정렬 알고리즘 (0) | 2022.07.06 |


