1) 개요
- 퀵 정렬은 원소 수가 n개인 입력 배열을 최악의 경우 O(n2)에 정렬하는 알고리즘이다.
퀵 정렬은 최악의 경우에는 수행시간이 느리지만, 평균 수행시간이 O(nlgn)으로 매우 효율적이고,
O(nlgn) 표현에 숨겨진 상수 인자도 매우 작다.
또한 내부 정렬이라는 장점도 있고, 가상 메모리 환경에서도 잘 동작해
일반적으로 실제 문제에서 가장 유용한 정렬 방법이다.
- 이 글에서는 퀵 정렬 알고리즘과 분할할 때 사용하는 중요한 서브 루틴을 설명한다.
퀵 정렬은 복잡한 알고리즘이기 때문에 성능에 관해 직관적인 논의롤 시작하고,
정확한 분석은 이 글의 끝으로 미룬다.
- 그 다음은 무작위 추출을 이용하는 랜덤화된 퀵 정렬을 소개한다.
이 알고리즘은 평균 수행시간이 적게 들고 모든 원소들이 서로 다르다면
특정한 입력 때문에 최악의 경우로 동작하는 일도 없다.
랜덤화된 알고리즘을 분석하며 최악의 경우 O(n2) 시간,
원소가 서로 다른 경우에 평균 O(nlgn) 시간에 동작함을 보인다.
2) 퀵 정렬
- 병합 정렬과 마찬가지로 퀵 정렬도 분할 정복에 기반을 두고 있다.
다음은 배열 A[p..r]을 처리하는 3단계 분할정복 과정이다.
분할: 배열 A[p..r]을 두 개의 부분 배열 A[p..q-1]과 A[q+1..r]로 분할(재배치)한다.
A[p..q-1]에는 A[q]보다 작거나 같은 원소를, A[q+1..r]에는 A[q]보다 크거나 같은 원소를 배치한다.
이 결과로 생기는 양쪽 부분 배열 중 한 쪽에는 아무 원소도 없을 수도 있다.
위의 분할 과정을 위한 인덱스 q를 계산한다.
정복: 퀵 정렬을 재귀 호출해서 A[p...q-1]과 A[q+1...r] 두 부분 배열을 정렬한다.
결합: 부분 배열이 이미 정렬되어 있으므로 따로 합치는 작업을 할 필요가 없다.
전체 배열 A[p...r]이 이미 정렬되어 있기 때문이다.
- 다음은 퀵 정렬을 구현한 프로시저다.
QUICKSORT(A, p, r)
if p < r
q = PARTITION(A, p, r)
QUICKSORT(A, p, q-1)
QUICKSORT(A, q+1, r)
- 전체 배열 A를 정렬하려면 QUICKSORT(A, 1, A.length)를 호출하면 된다.
3) 배열 분할
- 이 알고리즘의 핵심 부분은 부분 배열 A{p...r]을 내부에서 재배치하는 PARTITION 프로시저다.
PARTITION(A, p, r)
x = A[r]
i = p-1
for j = p to r-1
if A[j] <= x
i = i + 1
A[i] <-> A[j] 교환
A[i+1] <-> A[r] 교환
return i+1
- 그림 7.1은 원소 8개짜리 배열에 대한 PARTITION의 동작을 보여준다.
PARTITION은 항상 부분 배열 A[p..r]을 나눌 기준 원소로 x = A[r]을 선택한다.
프로시저가 진행되면서 배열은 네 구역으로 나누어진다(빈 구역이 생길 수 있다)
3-6행의 for 루프를 시작할 때마다 각 구역은 다음 루프 불변성을 만족한다.
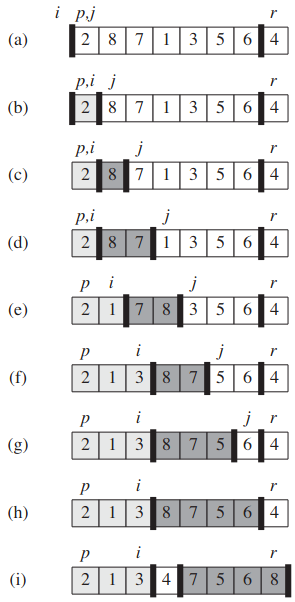
- 위의 그림은 예재 배열에 대한 PARTITION의 동작이다.
배열값 A[r]이 기준 원소 x로 사용된다. 옅게 칠해진 원소들은 모두 x보다 크지 않은 값으로 구성되는
첫 번째 구역에 속한다.
진한 회색 원소들은 x보다 큰 값으로 구성되는 두 번째 구역에 속한다.
흰색 원소들은 아직 앞쪽 두 구역 중 어디에 속하는지 결정되지 않은 것이다.
배열의 마지막에 있는 흰 원소가 기준 원소 x다.
(a) 배열과 변수의 초기 설정. 앞쪽 두 구역에 속한 원소는 없다.
(b) 2를 "자기 자신과 교환"하고 작은 값의 구역에 넣는다.
(c)-(d) 8과 7을 큰 값의 구역에 추가한다
(e) 1과 8을 교환하고 작은 값의 구역이 커진다.
(f) 3과 7을 교환하고 작은 값의 구역이 커진다.
(g) 큰 값의 구역에 5와 6을 포함시켜 커지게 하고 루프를 종료한다.
(i) 7-8의 행에서 기준 원소의 위치를 바꾸어 두 구역 사이에 가도록 한다.
- PARTITION의 마지막 두 행에서는 기준 원소를 x보다 큰 집합의 왼쪽 끝 원소와 교환하여
두 분할한 집합의 사이에 위치하도록 한 후 기준 원소의 변경된 인덱스를 리턴한다.
이제 PARTITION의 결과는 분할정복 과정 중 분할 단계에서 해야 할 일을 마친 상태다.
- 사실 이 결과는 좀 더 강한 조건을 만족한다.
QUICKSORT의 2행 이후에 A[q]가 A[q+1..r]의 모든 원소와 같을 수 없고, 무조건 작게 된다.
부분 배열 A[p..r]에 대한 PARTITION의 수행시간은 n = r - p + 1일 때 O(n)이다.
'Introduction to Algorithms' 카테고리의 다른 글
| [Introduction to Algorithms] 퀵 정렬 - 퀵 정렬의 성능 (0) | 2024.06.23 |
|---|---|
| [Introduction to Algorithms] 힙 만들기 (0) | 2024.06.23 |
| [Introduction to Algorithms] 힙 특성 유지하기 (0) | 2024.06.22 |
| [Introduction to Algorithms] 힙 정렬 알고리즘 (0) | 2024.06.21 |
| [Introduction to Algorithms] 위상정렬 (0) | 2024.06.21 |



